- Home
- Research at MPL
- Independent Research Groups
- Marquardt Research Group
- Research areas
Quantum Information Processing
By squeezing a light state the quantum uncertainty of one observable is reduced at the cost of a higher uncertainty in the conjugate observable. Apart from improving the sensitivity of metrological applications, squeezed states are used to create continuous variable entanglement which is a key ingredient for many quantum information tasks.
Polarization squeezing and entanglement
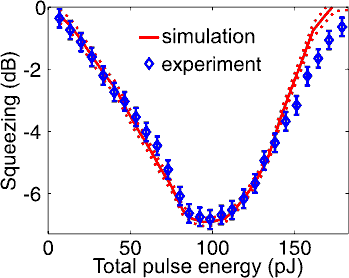
Non-classical polarization states of light are particularly interesting due to their compatibility with the spin variables of atomic systems and their simple detection without additional local oscillator. By exploiting the Kerr effect we generate efficient polarization squeezing using ultrashort light pulses in a single pass through a birefringent fiber [1]. Recently we have achieved a new world record in fiber squeezing: we have measured a noise reduction of -6.8±0.3 dB, which when corrected for linear losses is -10.4 ± 0.8 dB [2]. Applying first-principles simulations showed excellent agreement with these measurements (see Fig. 1) as well as with earlier ones [3]. By interfering two independent polarization squeezed light beams on a symmetric beam splitter we have generated a highly efficient and robust polarization entanglement source [4].
[1] J. Heersink, V. Josse, G. Leuchs, U. L. Andersen, Opt. Lett. 30, 1192 (2005)
[2] R.-F. Dong, J. Heersink, J. F. Corney, P. D. Drummond, U. L. Andersen, and G. Leuchs, Opt. Lett. 33, 116 (2008)
[3] J. F. Corney, P. Drummond, J. Heersink, V. Josse, G. Leuchs, and U.L. Andersen, Phys. Rev. Lett. 97, 023606 (2006)
[4] R.-F. Dong, J. Heersink, J. Yoshikawa, O. Glöckl, U. L. Andersen, and G. Leuchs, New J. Phys. 9 410 (2007)
Polarization squeezing and GAWBS in Photonic Crystal Fibers

An alternative tool for the generation of squeezed states are Photonic Crystal Fibers (PCFs) since the fiber’s microstructure allows for tailoring a multitude of parameters. For example, due to a higher non-linear effect the same amount of squeezing can be produced in a shorter fiber or with less power. Squeezed states thus accumulate less excess noise caused by phonon scattering [1], such as Guided Acoustic Wave Brillouin Scattering (GAWBS). Moreover, we have demon-strated that the microstructure of a PCF mechanically decouples the light-guiding fiber core from its environment. Less photon-phonon interactions thus lead to an additional GAWBS-noise reduction in commercially available PCFs (see Fig. 3) [2, 3]. Further improvements can be achieved by tailoring the microstructure.
[1] J. Milanovic, J. Heersink, Ch. Marquardt, A. Huck, U.L. Andersen, G. Leuchs, Las. Phys. 17, 559 (2007)
[2]D. Elser, U. L. Andersen, A. Korn, O. Glöckl, S. Lorenz, Ch. Marquardt, and G. Leuchs, Phys. Rev. Lett. 97, 133901 (2006)
[3]D. Elser, Ch. Wittmann, U. L. Andersen, O. Glöckl, S. Lorenz, Ch. Marquardt, and G. Leuchs, J. Phys.: Conf. Ser. 92, 012108 (2007)
Resonant and non-resonant interactions in filled hollow core Photonic Crystal Fibers

As an alternative to Kerr squeezing in fibers the high non-linearities of atoms at the resonance are promising. Self-induced transparency (SIT) can hereby prevent the light from being absorbed. We filled the core of hollow core PCFs with Rubidium (see Fig. 4) and plan to evaporate it to obtain a microscopic vapor cell. In addition to the generation of squeezing via SIT, filled hollow core fibers can act as a versatile tool for light-atom interactions.
Whispering Gallery Modes

We study nonlinear optical processes in whispering gallery mode (WGM) resonators to explore their quantum-optical aspects. The WGM resonators tend to have very high Q-factors as well as small optical mode volume, which greatly enhances the nonlinear frequency conversion processes. Such processes as e.g. second harmonic generation, parametric down-conversion, and others, then become efficient for very low optical powers and ultimately for individual photons. In this regime, the non-classical nature of the generated or converted light fields is most strongly revealed.
Cylindrically polarized modes of light
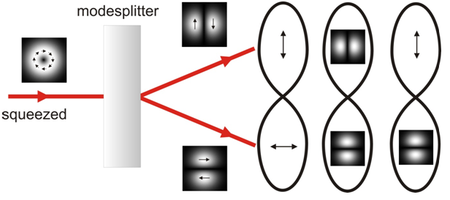
Cylindrically polarized modes have the intriguing property that they combine a complex polarization with a complex spatial pattern. In [1] we have shown that these two degrees of freedom (DOFs) are already inseparable in classical description of the modes. When a cylindrically polarized mode is quadrature squeezed this structural inseparability leads to entanglement not only in the polarization and spatial DOF but also between these two DOFs [2]. Currently we are working on the direct detection of this hybrid-entanglement [3]. Furthermore, we are investigating how these modes can be used for cluster state generation. Due to their unique properties they have the potential to generate cluster states which are compact and addressable. These are two features essential for successful quantum computing. In another experiment we are generating non-classical states of light in higher-order modes with the help of a spatial light modulator. This device allows one not only to generate cylindrically polarized modes, but also any desired higher-order mode.
[1] A. Holleczek, A. Aiello, C. Gabriel, Ch. Marquardt and G. Leuchs, Optics Express 19, 9714 (2011)
[2] C. Gabriel, A. Aiello, W. Zhong, T. G. Euser, N. Y. Joly, P. Banzer, M. Förtsch, D. Elser, U. L. Andersen, Ch. Marquardt, P. St.J. Russell and G. Leuchs, Phys. Rev. Lett. 106 (6), 060502 (2011)
[3] C. Gabriel, A. Aiello, S. Berg-Johansen, Ch. Marquardt, G. Leuchs, Eur. Phys. J D 66 (7) (2012) </p</p>
Quantum Key Distribution

Quantum key distribution (QKD) is the process of establishing a secret shared key between two parties, traditionally named Alice and Bob. The security is based on the laws of quantum mechanics, whereas in classical schemes security relies only on the unproven lack of efficient mathematical algorithms.
We have developed a QKD protocol which is particularly suitable for atmospheric transmission: we employ a local oscillator to perform an optical homodyne detection of weak coherent signal states. Alice utilizes polarization states to combine signal and local oscillator in a single beam. As a consequence, Bob’s detection is very efficient and perfectly shielded against any stray light.
We have experimentally demonstrated the feasibility of this protocol over a distance of 100m on the roof of the MPL building [1,2]. As the next step, we are now establishing a link of length 1.6km between the MPL and the University computer centre.
In contrast to entanglement based QKD schemes, our setup is of the prepare & measure type. Nevertheless Alice and Bob can model their correlations as if they shared an entangled state [3]. Bounds for sophisticated eavesdropping strategies like the manipulation of the local oscillator are derived in ongoing work with the group of Norbert Lütkenhaus. We also experimentally investigated the influence of a simple eavesdropping attack proved to be optimal for a certain class of QKD schemes [4].
Additionally, we have adapted our successful free-space cryptography scheme to fiber channels. In this setup, we were able to witness non-classical correlations between the sender and the receiver, so called effective entanglement [5].
[1] B. Heim, D. Elser, T. Bartley, M. Sabuncu, C. Wittmann, D. Sych, C. Marquardt und G. Leuchs, Appl. Phys. B, 98 (4), 635-640 (2010)
[2] D. Elser, T. Bartley, B. Heim, C. Wittmann, D. Sych und G. Leuchs, New Journal of Physics 11, 045014 (2009)
[3] S. Lorenz, J.Rigas, M. Heid, U.L. Andersen, N. Lütkenhaus und G. Leuchs, Phys. Rev. A 74, 042326 (2006)
[4] M. Sabuncu, L. Mista, Jr.,J. Fiurásek, R. Filip, G. Leuchs, U.L. Andersen, Phys. Rev. A 76, 032309 (2007)
[5] C. Wittmann, J. Fürst, C. Wiechers, D. Elser, H. Häseler, N. Lütkenhaus, und G. Leuchs Optics Express 18, 4499 (2010)
Quantum Hacking
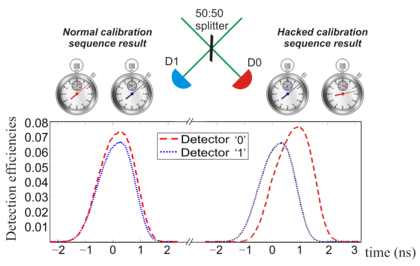
Any practical QKD implementation suffers from imperfections, such as flaws in the source and/or detector(s). These could be exploited by an eavesdropper Eve to obtain information about the secret key without being discovered. With secure quantum communication poised to be the first successful commercially-deployed application of quantum information processing, it becomes increasingly important to verify the actual level of security in the implementations. We experimentally review an off-the-shelf commercial system from ID Quantique to identify loopholes and exploit vulnerabilities by simulating and performing attacks on it. The principal idea is to secure the system in a regenerative sense, so we also propose patches and countermeasures, wherever possible. In this project, we collaborate with the Quantum Hacking group situated at IQC Waterloo in Canada.
So far, we have been able to successfully compromise the security of the system by launching a variety of faked-state attacks. Using tailored bright illumination to blind the detectors [1], Eve can dictate the measurements performed by Bob and thus, obtain a perfect copy of the raw key while remaining virtually undetected. A more sophisticated version of this employs heating the APDs with bright illumination. Since this thermal blinding [2] can be done well in advance of the actual key-exchange frames, it is as such harder to catch. We recently also tested another method to control the detection events by sending bright pulses outside the gated region in Bob [3]. A video abstract explaining the basic concepts behind this attack has been made by our team (see right side).
We have also been able to exploit a vulnerability in the implementation of a vital calibration sequence of this commercial QKD system that allows Eve to induce a detector efficiency mismatch (refer figure 2). We demonstrate an optimized faked-state attack on such a hacked system that would cause a QBER below 7% without any reduction in Bob’s expected detection rate for a large range of expected channel transmissions. Most recently, a generalized version of tailored bright illumination that exploits superlinear characteristics of single-photon detectors based on APDs and superconducting nanowires has also been demonstrated [5].
[1] L. Lydersen, C. Wiechers, C. Wittmann, D. Elser, J. Skaar and V. Makarov, Nature Photonics 4, 686 (2010)
[2] L. Lydersen, C. Wiechers, C. Wittmann, D. Elser, J. Skaar and V. Makarov, Opt. Express 18 (26), 27938-27954 (2010)
[3] C. Wiechers, L. Lydersen, C. Wittmann, D. Elser, J. Skaar, Ch. Marquardt, V. Makarov and G. Leuchs, New Journal of Physics 13 (1), 013043 (2011)
[4] N. Jain, C. Wittmann, L. Lydersen, C. Wiechers, D. Elser, Ch. Marquardt, V. Makarov and G. Leuchs, Phys. Rev. Lett. 107, 110501 (2011)
[5] L. Lydersen, N. Jain, C. Wittmann, Ø. Marøy, J. Skaar, Ch. Marquardt, V. Makarov and G. Leuchs, Phys. Rev. A. 84, 8 (2011)
Quantum Cloning
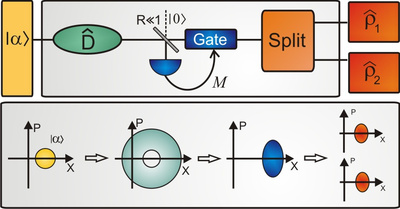
Due to the linearity of quantum mechanics it is impossible to perfectly clone an arbitrary quantum state. It is however interesting to find the best possible cloning device, i.e. an optimal distributor of quantum information. Our group has already implemented several quantum cloners for coherent states [1–3] that operate at the quantum limit.
In all these implementations, the clones are generated by first amplifying and subsequently splitting the input state. Thereby, the quality of the clones is limited by the inevitable noise penalty imposed by the amplification process. However, this noise penalty can be largely suppressed in a probabilistic setting.
In a recent experiment we could show that the cloning fidelity between a coherent input state and its clones can be pushed beyond the (deterministic) quantum limit in a probabilistic scheme [4]. In the conducted experiment, a schematic of which is shown on the right, coherent states from a phase-covariant alphabet were first subject to a specifically tailored random displacement. Subsequently, a photon number resolving measurement on a small tapped-off part of the state is performed and the remaining part of the state is post-selected based on the outcome of this measurement. This results in a probabilistic noiseless amplification of the state and enables the generation of clones with qualities beyond the deterministic quantum limit.
[1] V. Josse, M. Sabuncu, N. Cerf, G. Leuchs, and U. L. Andersen, Phys. Rev. Lett. 96, 163602 (2006)
[2] M. Sabuncu, U.L. Andersen, G. Leuchs, Phys. Rev. Lett. 98, 170503 (2007)
[3] M. Sabuncu, G. Leuchs, U.L. Andersen, Phys. Rev. A 78, 052312 (2008)
[4] C. R. Müller, C. Wittmann, P. Marek, R. Filip, Ch. Marquardt, G. Leuchs, and U.L. Andersen, Phys. Rev. A 86, 010305(R) (2012)
Quantum Amplification
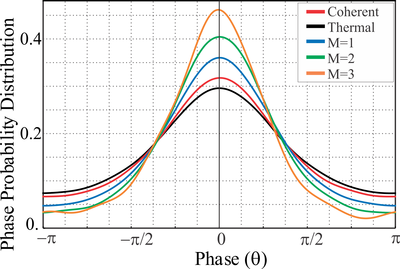
In the continuous variable regime, the bounds imposed by the laws of quantum mechanics are formulated in terms of ensemble statistics and hence are of a statistical nature. Consequently, these laws need not hold true for every individual observation of a quantum state.
On the basis of this insight, we could show that the phase information carried by coherent states can be increased probabilistically – an operation forbidden for deterministic operations. Interestingly, in the experimentally implemented scheme a source of thermal noise, usually causing decoherence and hence the loss of information, serves as the driving element of the information enhancement. After the noise addition, a suitably chosen measurement on a small part of the state provides an indicator for the information content of the state at hand, such that only the well-processed states are kept while the others are discarded [1]. The experimental results show a significant reduction of the phase uncertainty, which is equivalent to enhanced phase information.
[1] M. A. Usuga, C. R. Müller, C. Wittmann, P. Marek, R. Filip, Ch. Marquardt, G. Leuchs and U. L. Andersen, Nature Physics 6 (10), 767-771 (2010)
For applications in quantum information protocols we are performing research on optimal single measurements of quantum states. The full characterization of quantum states additionally requires reconstruction techniques, which derive the information from measurements on an ensemble of identical states.
Quantum Random Number Generator

Quantum random number generators have the potential to deliver truly random numbers, an important attribute for many applications ranging from simulations over gambling to cryptography. Our random number generator [1] measures the noise of the electric field variables of a vacuum state. This can be realized with a simple homodyne setup. By appropriately post-processing the measured date, truly random numbers which are solely based on quantum noise can be extracted. Samples of our truly random numbers can be downloaded here: 50MB, 200MB
[1] Christian Gabriel, Christoffer Wittmann, Denis Sych, Ruifang Dong, Wolfgang Mauerer, Ulrik L. Andersen, Christoph Marquardt, Gerd Leuchs Nature Photonics. 4, 711-715 (2010)
Tomography of polarization squeezed states
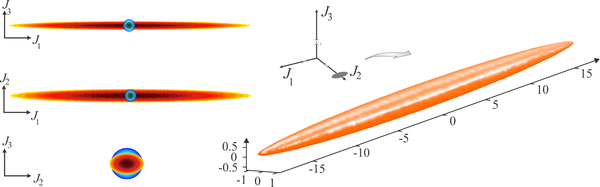
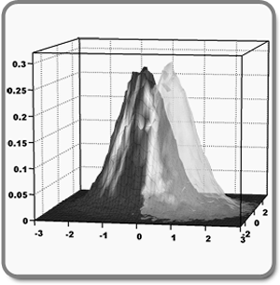
Polarization states of the light field are conveniently described in the Stokes space, which is spanned by the Stokes vectors. In the quantum mechanical treatment, the Stokes space is not continuous, but is composed of a set of nested spheres. A polarization state is generally distributed over several of these spheres. However, in the case of a bright and localized state, the state can be approximated to lie in a quasi-continuous and flat space.
We could show explicitly that the state reconstruction is then equivalent to the inverse Radon transformation from projections of the state along all directions in Stokes space. This technique, however, is statistically unstable and is likely to produce unphysical features in the reconstructed state. As an alternative, we have proposed a novel maximum likelihood reconstruction (ML) and compared the two techniques for the reconstruction of a bright polarization squeezed state [1]. A visual perspective of how we perform this reconstruction can be obtained from the video abstract shown on the right. Thereby, we could show that the ML technique allows us to get reconstructions of the same quality but from data sets which are two orders of magnitude smaller than required for the inverse Radon reconstruction. The results of the technique are shown in the figure below.
[1] C. R. Müller, B. Stoklasa, C. Peuntinger, C. Gabriel, J. Řeháček, Z. Hradil, A. B. Klimov, G. Leuchs, Ch. Marquardt, and L. L. Sánchez-Soto, New Journal of Physics 14, 085002 (2012)
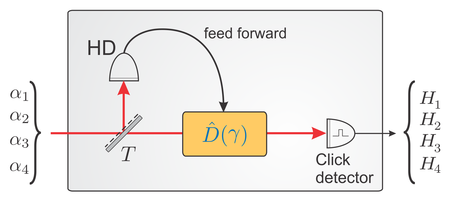
Novel Quantum Receivers
Quantum state discrimination is one of the fundamental issues in optical communication and quantum signal detection. An important figure of merit here is the error rate. For a pair of coherent states, homodyne detection represents an effective way to achieve near-minimal error discrimination. A receiver based on photon counting would lead to even smaller error rates, provided if signal intensities are sufficiently large. In order to outperform the homodyne scheme also for smaller photon numbers, we have succesfully implemented a novel detection schemes [1–4].
In our latest work on quantum state discrimination, we experimentally demonstrated a hybrid discrimination scheme for quadrature phase-shift keyed quantum signals (QPSK) which outperforms the standard scheme – heterodyne detection – for any signal power [5]. The QPSK alphabet comprises four states with identical amplitude but separated by a relative phase shift of π/2 and is used for instance by the HSDPA protocol in UMTS networks for mobile phones, in digital satellite communication and in backbone fiber networks.
For the identification of the input state, the signal is divided on a beam splitter and the parts are guided to a homodyne receiver and a photon detector, respectively. First, the homodyne detector performs an adequate quadrature measurement that allows to discard half of the candidate states. The result is forwarded to a second receiver stage where it is used to optimally tune a displacement prior to a photon detector which finally discriminates between the remaining pair of states.
Interestingly, the discrimination in our scheme is carried out by a hybrid receiver addressing both the continuous variable (homodyne detection) and the discrete variable (photon detection) representation of the signal states.
[1] C. Wittmann, M. Takeoka, Katiuscia N. Cassemiro, M. Sasaki, G. Leuchs, and U. L. Andersen, Phys. Rev. Lett 101, 210501-4 (2008)
[2] C. Wittmann, U. L. Andersen, and G. Leuchs, J. Mod. Opt. 57, 213 (2010)
[3] C. Wittmann, U. L. Andersen, M. Takeoka, D. Sych, and G. Leuchs, Phys. Rev. Lett 104, 100505 (2010)
[4] C. Wittmann, U. L. Andersen, M. Takeoka, D. Sych, and G. Leuchs, Phys. Rev. A 81, 062338 (2010)
[5] C. R. Müller, M. A. Usuga, C. Wittmann, M. Takeoka, Ch. Marquardt, U. L. Andersen, and, G. Leuchs, New Journal of Physics 14, 083009 (2012)
© Max Planck Institute for the Science of Light





