Durch Quetschen eines Lichtzustands wird die Quantenunschärfe einer Observablen reduziert. Dies geschieht allerdings auf Kosten einer größeren Unschärfe in der konjugierten Observablen. Neben der Erhöhung der Empfindlichkeit messtechnischer Anwendungen werden gequetschte Zustände genutzt, um Verschränkung mit kontinuierlichen Variablen zu erzeugen, ein Hauptbestandteil vieler Quanteninformationsanwendungen.
Polarisationsgequetschtes Licht und Verschränkung
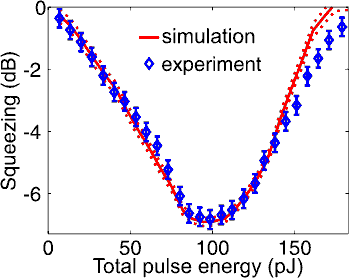
Simulationen auf der Basis von Grundprinzipien erklären die Resultate vollständig [3].
Nichtklassische Polarisationszustände des Lichts sind von besonderer Bedeutung aufgrund ihrer Kompatibilität mit den Spin-Variablen atomarer Systeme und ihrer einfachen Detektion ohne zusätzlichen Lokaloszillator. Unter Ausnutzung des Kerr-Effekts erzeugen wir effizient polarisationsgequetschtes Licht durch Propagation ultrakurzer Lichtpulse durch eine doppelbrechende Faser [1]. Vor kurzem erzielten wir einen neuen Weltrekord in der faserbasierten Erzeugung gequetschter Zustände: Wir haben eine Verringerung des Rauschens um -6,8±0,3 dB gemessen, was abzüglich der linearen Verluste einen Wert von –10,4±0,8 dB ergibt [2]. Der Vergleich mit Simulationen auf der Basis von Grundprinzipien ergab hervorragende Übereinstimmungen, sowohl mit diesen Messungen (vgl. Abb. 1), als auch mit früheren [3]. Durch Interferenz zweier unabhängiger polarisationsgequetschter Lichtstrahlen an einem symmetrischen Strahlteiler haben wir eine höchst effiziente und robuste Quelle für Polarisationsverschränkung aufgebaut [4].
[1] J. Heersink, V. Josse, G. Leuchs, U. L. Andersen, Opt. Lett. 30, 1192 (2005)
[2] R.-F. Dong, J. Heersink, J. F. Corney, P. D. Drummond, U. L. Andersen, and G. Leuchs, Opt. Lett. 33, 116 (2008)
[3] J. F. Corney, P. Drummond, J. Heersink, V. Josse, G. Leuchs, and U.L. Andersen, Phys. Rev. Lett. 97, 023606 (2006)
[4] R.-F. Dong, J. Heersink, J. Yoshikawa, O. Glöckl, U. L. Andersen, and G. Leuchs, New J. Phys. 9 410 (2007)
Polarisationsgequetschte Zustände und GAWBS in photonischen Kristallfasern

verhindern, dass unerwünschte akustischen Vibrationen in den lichtleitenden Kern eindringen [2].
Eine weitere Methode gequetschte Zustände zu erzeugen sind photonische Kristallfasern (photonic crystal fibers, PCFs), wobei durch die Mikrostruktur der Faser eine Vielzahl von Parametern modifiziert werden kann. Beispielsweise kann aufgrund eines höheren nichtlinearen Effekts der gleiche Quetschgrad mit einer kürzeren Faser oder mit geringerer Leistung erreicht werden. Auf diese Weise häufen gequetschte Zustände weniger Rauschen durch Phononenstreuung, wie zum Beispiel GAWBS (guided acoustic wave brillouin scattering) an [1]. Des weiteren haben wir gezeigt, dass die Mikrostruktur einer PCF den lichtleitenden Faserkern von seiner Umgebung mechanisch entkoppelt. Daher führen geringere Photon-Phonon-Wechselwirkungen zu einer zusätzlichen Verringerung des GAWBS-Rauschens in kommerziell erhältlichen PCFs (vgl. Abb .3) [2, 3]. Durch Anpassen der Mikrostruktur können weiterreichende Verbesserungen erreicht werden.
[1] J. Milanovic, J. Heersink, Ch. Marquardt, A. Huck, U.L. Andersen, G. Leuchs, Las. Phys. 17, 559 (2007)
[2] D. Elser, U. L. Andersen, A. Korn, O. Glöckl, S. Lorenz, Ch. Marquardt, and G. Leuchs, Phys. Rev. Lett. 97, 133901 (2006)
[3] D. Elser, Ch. Wittmann, U. L. Andersen, O. Glöckl, S. Lorenz, Ch. Marquardt, and G. Leuchs, J. Phys.: Conf. Ser. 92, 012108 (2007)
Resonante und nicht-resonante Wechselwirkungen in gefüllten Hohlkern-PCFs

Die hohe Nichtlinearität von Atomen nahe der Resonanz ist eine vielversprechende Alternative zur Kerr-Nichtlinearität in Fasern. Selbstinduzierte Transparenz (SIT) kann dabei die Absorption von Licht verhindern. Wir haben den Hohlkern von PCFs mit Rubidium gefüllt (vgl. Abb. 4) und planen, daraus eine mikroskopische Gaszelle herzustellen. Außer der Erzeugung gequetschter Zustände durch SIT dienen Hohlkernfasern auch als vielseitiges Hilfsmittel für die Untersuchung von Atom-Licht-Wechselwirkungen.
Whispering Gallery Modes

Wir untersuchen nichtlineare optische Prozesse und ihre quantenoptischen Aspekte in "Whispering Gallery Mode" (WGM) Resonatoren. Diese können sowohl einen sehr großen Q-Faktor als auch eine kleines optisches Modenvolumen besitzen. Dadurch werden die nichtilnearen Frequenzkonversions-Prozesse deutlich verstärkt. Beispielsweise werden Prozesse wie "Second Harmonic Generation" und "Parametric Down Conversion" schon für sehr geringe optische Leistungen, und letztenendes sogar für einzelne Photonen, effizient. In diesem Regime tritt die nichtklassische Natur des erzeugten und konvertierten Lichtfeldes zu Tage.
Quanten-Schlüsselverteilung

Quanten-Schlüsselverteilung (quantum key distribution, QKD) ist die Erzeugung eines gemeinsamen, geheimen Schlüssels zwischen zwei Parteien, die normalerweise Alice und Bob genannt werden. Die Sicherheit liegt dabei in den Gesetzen der Quantenmechanik begründet, im Gegensatz zu unbewiesenen mathematischen Annahmen bei klassischen Verfahren. In unserem Freistrahl-QKD-Aufbau kodieren wir das Signal in kohärente Zustände, die einfache und schnelle Zustands-Präparation und -Messung ermöglichen. Wir benutzen ein Paar konjugierter Polarisations-Variablen (Stokes-Parameter) als Signalträger. Dadurch erreichen wir beim Empfänger einen ausgezeichneten Interferenzkontrast, der keiner Stabilisierung bedarf. Nach der erfolgreichen Demonstration dieses QKD-Schemas im Labor arbeiten wir nun an Steigerungen von Pulsrate und Übertragungsdistanz. Wir haben eine Freiraumverbindung über eine Entfernung von 100m auf dem Dach unseres Institutsgebäudes aufgebaut, die es uns ermöglicht atmosphärische Effekte für die QKD mit kontinuierlichen Variablen zu quantifizieren. In dieser Machbarkeitsstudie befinden sich, aus Gründen der Einfachheit, Alice´ und Bobs Station auf dem selben optischen Tisch. Der Lichtstrahl wird auf das Dach gesendet und nach 50m von einem Retro-Reflektor zurückgeworfen (vgl. Abb. 1). Die Ergebnisse wurden in [1,2] veröffentlicht. Als nächsten Schritt wollen wir eine wirkliche Punkt-zu-Punkt Verbindung im Kilometerbereich aufbauen. Im Gegensatz zu verschränkungsbasierten QKD-Schemata ist unser Aufbau vom Typ „Präparation & Messung“. Dennoch können Alice und Bob ihre Korrelationen modellieren, als ob sie einen verschränkten Zustand teilen würden [3]. In Zusammenarbeit mit der Gruppe von Norbert Lütkenhaus bestimmen wir Kriterien gegen ausgeklügelte Abhörstrategien, wie z.B. eine Manipulation des Lokaloszillators (vgl. Abb. 2). Vor kurzem haben wir zudem einen einfachen Lauschangriff, der für bestimmte Klassen von QKD-Schemata bewiesenermaßen optimal ist, experimentell untersucht [4]. Zusätzlich haben wir unser Freistrahl-QKD-Schema auch erfolgreich auf einen Glasfaserkanal angepasst. In diesem Experiment konnten wir nichtklassische Korrelationen zwischen Sender und Empfänger nachweisen, eine sogenannte "effektive Verschränkung" [5].
[1] B. Heim, D. Elser, T. Bartley, M. Sabuncu, C. Wittmann, D. Sych, C. Marquardt und G. Leuchs, Appl. Phys. B, 98 (4), 635-640 (2010)
[2] D. Elser, T. Bartley, B. Heim, C. Wittmann, D. Sych und G. Leuchs, New Journal of Physics 11, 045014 (2009)
[3] S. Lorenz, J.Rigas, M. Heid, U.L. Andersen, N. Lütkenhaus und G. Leuchs, Phys. Rev. A 74, 042326 (2006)
[4] M. Sabuncu, L. Mista, Jr.,J. Fiurásek, R. Filip, G. Leuchs, U.L. Andersen, Phys. Rev. A 76, 032309 (2007)
[5] C. Wittmann, J. Fürst, C. Wiechers, D. Elser, H. Häseler, N. Lütkenhaus, und G. Leuchs Optics Express 18, 4499 (2010)
Quantenklonen
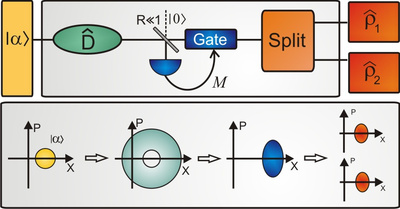
Aufgrund der Linearität der Quantenmechanik ist es unmöglich einen beliebigen Quantenzustand perfekt zu klonen. Es ist aber interessant, die bestmögliche Klonmaschine zu entwickeln, d.h. einen optimalen Verteiler von Quanteninformation. Basierend auf einem quantenrauschbegrenzten Verstärker hat unsere Gruppe einen nahezu optimalen Quantenkloner für kohärente Zustände realisiert [1]. Des Weiteren haben wir gezeigt, dass die Leistung des Kloners weiter erhöht werden kann, wenn er mit Paaren phasenkonjugierter kohärenter Zustände oder zusätzlicher a-priori Information über den Eingangszustand versorgt wird (vgl. Abb. 2)[2, 3].
[1] V. Josse, M. Sabuncu, N. Cerf, G. Leuchs, and U. L. Andersen, Phys. Rev. Lett. 96, 163602 (2006)
[2] M. Sabuncu, U.L. Andersen, G. Leuchs, Phys. Rev. Lett. 98, 170503 (2007)
[3] M. Sabuncu, G. Leuchs, U.L. Andersen, Phys. Rev. A 78, 052312 (2008)
[4] C. R. Müller, C. Wittmann, P. Marek, R. Filip, Ch. Marquardt, G. Leuchs, and U.L. Andersen, Phys. Rev. A 86, 010305(R) (2012)
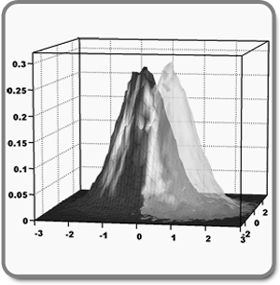
Für die Anwendung von Quanteninformationsprotokollen untersuchen wir Einzelmessungen von Quantenzuständen. Zur vollständigen Charakterisierung von Quantenzuständen bedarf es weiterer Rekonstruktionstechniken, welche Information aus Messungen von einem Ensemble identischer Zustände generieren.
Quantenzufallszahlengenerator

Quantenzufallszahlengeneratoren haben das Potential echt zufällige Zahlen zu erstellen. Dies ist für viele verschiedene Anwendungen von großer Wichtigkeit, u.a. für Simulationen oder Kryptographie. Unser Zufallszahlengenerator [1] misst das Rauschen eines Vakuumzustandes, wofür ein einfacher homodyne Detektor benutzt wurde. Die Daten werden entsprechend nachbearbeitet um sicher zu gehen, dass nur Quantenrauschen benutzt wurde, um Zufallszahlenen zu generieren.
[1] Christian Gabriel, Christoffer Wittmann, Denis Sych, Ruifang Dong, Wolfgang Mauerer, Ulrik L. Andersen, Christoph Marquardt, Gerd Leuchs Nature Photonics. 4, 711-715 (2010)
Tomographie polarisationsgequetscher Zustände
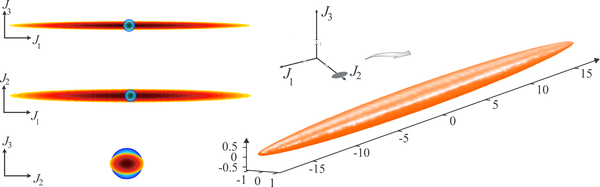
Bisher wurde polarisationsgequetschtes Licht allein durch die Varianzen der Stokes-Parameter charakterisiert. Mittels unserer faserbasierten Quelle gequetschten Lichts konnten wir erstmalig eine vollständige Rekonstruktion eines polarisationsgequetschten Zustands durchführen(vgl. Abb. 2)
[1] C. R. Müller, B. Stoklasa, C. Peuntinger, C. Gabriel, J. Řeháček, Z. Hradil, A. B. Klimov, G. Leuchs, Ch. Marquardt, and L. L. Sánchez-Soto, New Journal of Physics 14, 085002 (2012)
Neuartige Quantenempfänger
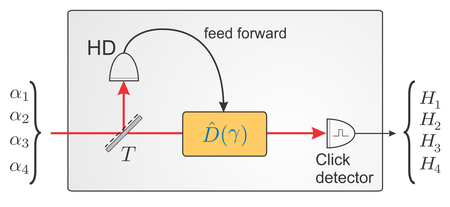
Quantenzustandsunterscheidung ist grundlegend für optische Kommunikation und Quantensignaldetektion. Ein wichtiges Qualitätskriterium stellt dabei die Fehlerrate dar. Für ein Paar kohärenter Zustände stellt die Homodyndetektion eine effektive Art dar, Quantenzustände mit nahezu minimalem Fehler zu unterscheiden. Ein auf Photonenzählung basierender Empfänger führt bei ausreichend hoher Signalintensität zu noch kleineren Fehlerraten. Um auch bei kleineren Intensitäten eine Verbesserung gegenüber der Homodyndetektion zu erreichen, bauen wir momentan einen neuartigen Quantenempfänger auf.
[1] C. Wittmann, M. Takeoka, Katiuscia N. Cassemiro, M. Sasaki, G. Leuchs, and U. L. Andersen, Phys. Rev. Lett 101, 210501-4 (2008)
[2] C. Wittmann, U. L. Andersen, and G. Leuchs, J. Mod. Opt. 57, 213 (2010)
[3] C. Wittmann, U. L. Andersen, M. Takeoka, D. Sych, and G. Leuchs, Phys. Rev. Lett 104, 100505 (2010)
[4] C. Wittmann, U. L. Andersen, M. Takeoka, D. Sych, and G. Leuchs, Phys. Rev. A 81, 062338 (2010)
[5] C. R. Müller, M. A. Usuga, C. Wittmann, M. Takeoka, Ch. Marquardt, U. L. Andersen, and, G. Leuchs, New Journal of Physics 14, 083009 (2012)
© Max Planck Institute for the Science of Light